有趣的turtle

27 May 2018

Reading time ~1 minute

偶然想起很早以前在小学读物里看到的神奇的logo语言，可以用来绘制一些很有趣的图案，python自带了一个turtle库实现了logo语言的功能，心血来潮用这个库玩了下。

绘制一棵树

from turtle import Turtle
from typing import Union

DEPTH = 4

pen = Turtle()
screen = pen.getscreen()
pen.begin_fill()


def draw_tree(level: int, pos: tuple = (0, 0), angle: int = 90, pen_color: Union[str, tuple] = 'brown') -> None:
    """
    :param level: 层级
    :param pos: 起点
    :param angle: 角度
    :param pen_color: str or tuple represents the color, such as 'green', '#ffffff', (12,30,33)
    :return:
    """
    pen.pencolor(pen_color)
    if level > DEPTH:
        return
    pen.up()
    pen.goto(pos)
    pen.down()
    pen.setheading(angle)
    pen.forward(30)
    angle = pen.heading()
    pos = pen.pos()
    # 设置叶子节点颜色
    color = 'green' if level == DEPTH - 1 else 'brown'
    # 回到上一个位置并绘制下一个分支
    draw_tree(level + 1, pos, angle+20, color)
    draw_tree(level + 1, pos, angle-20, color)
    if not pen.filling():
        pen.end_fill()


if __name__ == '__main__':
    draw_tree(0)
    pen.hideturtle()
    screen.mainloop()

tree

很简陋的绘画O(∩_∩)O，过程很简单就是利用类似二叉树的深度遍历的递归实现。

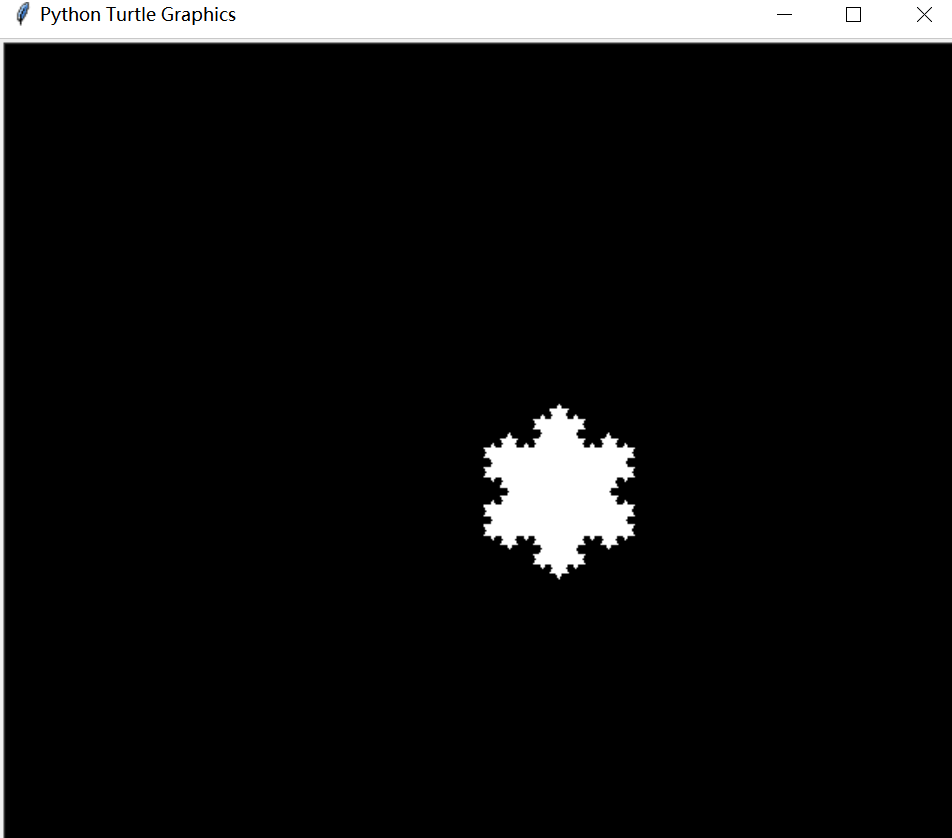
绘制科赫曲线

from turtle import Turtle

pen = Turtle()
screen = pen.getscreen()
screen.bgcolor('black')
pen.color('white', 'white')


def koch(length: float, level: int) -> None:
    """
    根据科赫曲线，每次将要绘制的线段进行三等分切割，并从第二段构建一个新的等边三角形
    :param length:  长度
    :param level:  当前分割次数
    :return:
    """
    if level < 1:
        pen.forward(length)
    else:
        koch(length / 3, level - 1)
        pen.left(60)
        koch(length / 3, level - 1)
        pen.right(120)
        koch(length / 3, level - 1)
        pen.left(60)
        koch(length / 3, level - 1)


def draw_koch(length: float, level: int) -> None:
    """
    绘制科赫曲线
    :param length: 初始的等边三角形边长
    :param level:  分割绘制次数
    :return:
    """
    pen.begin_fill()
    for _ in range(3):
        koch(length, level)
        pen.right(120)
    pen.end_fill()
    pen.hideturtle()


if __name__ == '__main__':
    draw_koch(100, 3)
    pen.screen.mainloop()

koch snow flake

通过每次将长度三等分，并重新生成一个等边三角形，通过递归就可以实现。

python 图形 turtle logo